Two Moment Simulation - Mean and variance

This article will look into how to simulate a series which has normal distribution i.e. higher moments ( Skew, Excess Kurt ) is 0. for simulation with 4 moments refer to this article
In the first part, we will look into the case of 1 dimension. in the second ,we will see how to incorporate covariance for more than 1 dimension.

Univariate simulation ( 1 Dimension )

Idea is to simulate a series

if $\mu$ and $\sigma$ are given.

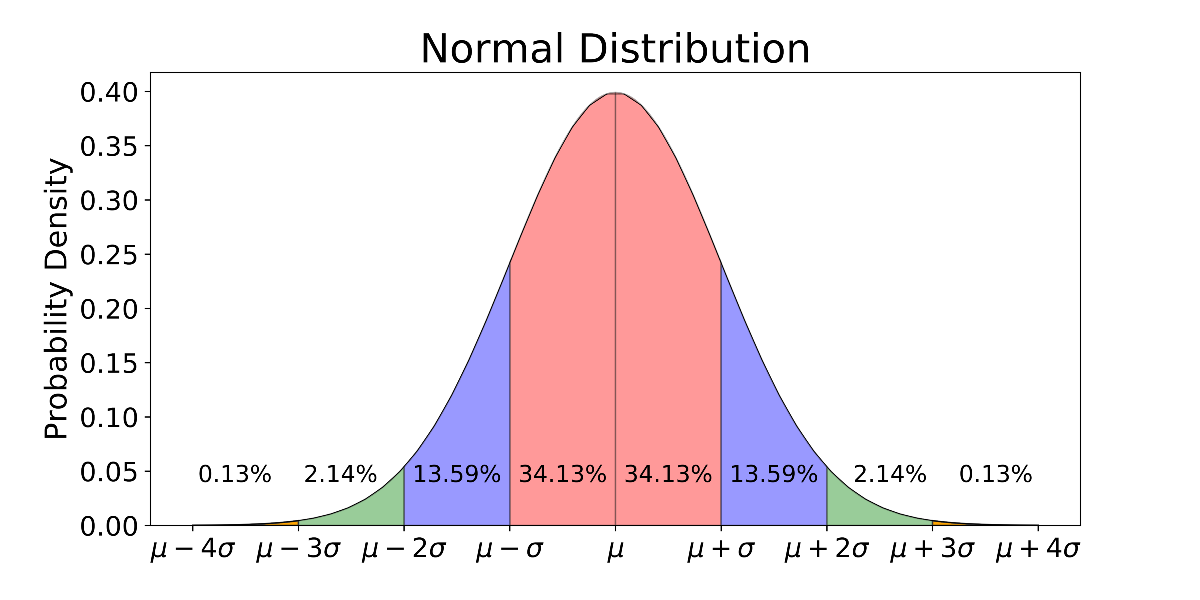
probability distribution for a R.V. that has a normal distribution. every point
$x_{i}$ = $\mu$ + z $\times$ $\sigma$ where z $\in$ ($-\infty$, $\infty$)

To generate N(0,1) we can use Box-Muller transformation.
in excel:

NORM.S.INV(rand()), rand() is from univform dist.(0,1), NORM.S.INV is inverse of cumulative normal distribution  

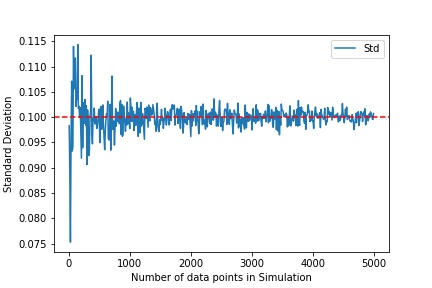
number of simulation / data points is critical to accuracy of the simulation. higher data points will lead to higher accuracy.

Higher accuracy to expected mean and variance with less data points discussed here using random matrix theory

Multivariate simulation ( >1 Dimension )

Idea is to simulate a series

if $M$ = array of mean and $\Sigma$ = covariance are given.

$\sqrt{\Sigma} =L$ is cholskey decomposition of $\Sigma = LL^{T}$