Four Moment Simulation - Mean, Variance, Skew, Kurtosis
In the previous article we discussed how to simulate normal distribution points for a given mean and standard deviation / covariance matrix
Here, we will discuss how to generate non normal numbers with unimodal distribution i.e. simulate using all four moments ( mean , standard deviation, skewness and kurtosis ) ignoring coskewness and cokurtosis
We refer to paper by Hao Luo[1], which uses Fleishman’s power method[2] to simulate non normal data
The idea is to first simulate a series Y using power method
\[Y \sim D(0,1, \gamma_{1}, \gamma_{2})\]where $\gamma_{1}$, $\gamma_{2}$ is the skewness and excess kurtosis of the distribution D, resp.
Second, we will use our understanding from previous article to covert first two moments of D from [0,1] to [$\mu$ , $\sigma$ / $\Sigma$]
Algo:
As per power method, Y can be defined as the third degree polynomial of X
\[Y = a + bX + cX^{2} + dX^{3}\]where $X \sim N(0,1)$
we would solve for
\[E(Y) = 0 , E(Y^{2}) = 1, E(Y^{3}) = \gamma_{1}, E(Y^{4}) = \gamma_{2} + 3\]The following 4 equations we got by solving the above equations:
\[F_1(b,c,d) : b^2+6bd+ 2c^2 +15d^2-1 =0\] \[F_2(b,c,d) : 2c(b^2+24bd+105d^2+2)-\gamma_1=0\] \[F_3(b,c,d) : 24(bd + c^2[1 + b^2 + 28bd] + d^2[12 + 48bd + 141c^2 + 225d^2])-\gamma_2 = 0\] \[a = -c\]To solve for a,b,c,d:
\(minimize F(b,c,d) = F_1^2(b,c,d)+F_2^2(b,c,d)+F_3^2(b,c,d)\) constrained on
\[F_i(b,c,d) =0 \forall i \in (1,3)\]Solution for above only exist when
\[\gamma_2 = −1.2264489 + 1.6410373 \gamma_1^2\]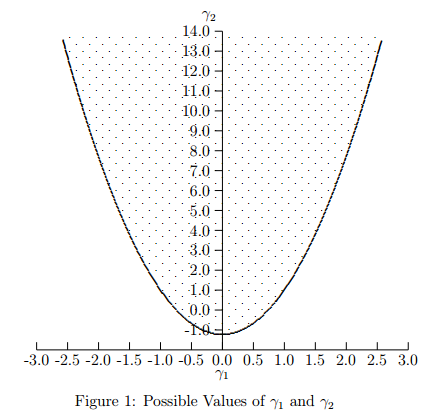
Finally, apply the transformation:
\[Y[\mu, \Sigma, \gamma_1, \gamma_2] = \mu + \sqrt{\Sigma} \times Y[0, 1, \gamma_1, \gamma_2]\]Results:
Let’s try to simulate beta distribution with $\alpha$ = 4.5 and $\beta$ = 1. The Left chart shows PDF of Beta , Simulated beta using above methodology and Normal distribution with mean = $\mu$($\beta$($4.5,1$)), std = $\sigma$($\beta$($4.5,1$)). right chart shows the cumulative distribution of the same except Nomral.
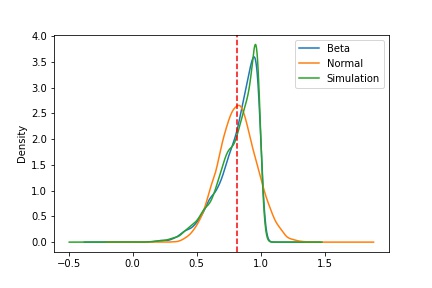
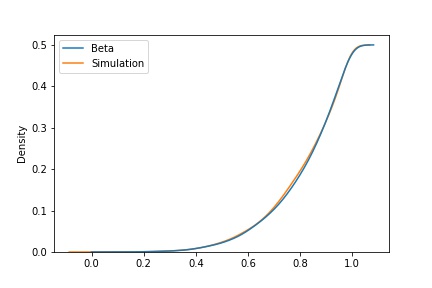
Pdf and it’s Cummulative distribution is very close to each other KS statstic of the same.
Table with first four moment values for all 3 cases:
| Stats | Beta | Normal | Simulation |
|---|---|---|---|
| Mean | 0.82 | 0.82 | 0.81 |
| Std | 0.15 | 0.15 | 0.15 |
| Skew | -1.13 | 0 | -1.08 |
| Kurt | 1.02 | 0 | 0.88 |
Link:
[1] Hao Luo (2011). Generation of Non-normal Data – A Study of Fleishman’s Power Method. here
[2] Fleishman, A. I. (1978). A method for simulating non-normal distributions.Psychometrika. here

Comments